Pythagoras of Samos (570 – 500 B.C.)
Pythagoras himself: The biography of Pythagoras is shrouded in legend where the stories about him and his followers seem better than the actual truth — which is unfortunately lost to history. Like Thales, he in known to us through the writings of others. Here are some basic, if not vague facts, about Pythagoras. He was born the son of a merchant about 572 B.C. in Samos. Pythagoras may have studied under Thales and may have even travel to Egypt to study their geometry. He returned to Samos, which at that time was under the direction of tyrannical governments, and ultimately decided to settle in the Italian town of Croton where he founded his famous Pythagorean school. The Pythagoreans were a brotherhood of thinkers and often religious zealots complete with secret rites and mysterious rituals. As such, they wound up making enemies, were persecuted, and their school buildings were destroyed. They were eventually dispersed, with Pythagoras possibly going to Metapontum, where he died (or was possibly murdered), but the movement lasted for many years afterward and their influence was felt throughout Western thought. Read more about Pythagoras and his followers.
His followers: The Pythagoreans believed that the seemingly chaotic world could be understood through numbers – namely ratios of whole numbers. For example, through experimentation, they discovered that musical harmony can be understood through ratios of whole numbers. When a string is plucked and then plucked again but with the players finger half way up the string, the result is an octave. Another important contribution of the Pythagoreans was their belief that one can do mathematics purely for its own sake. It does not have to have a practical application. In fact, abstract thinking was a link to the eternal.
The Pythagorean theorem: Mathematics was a vital part of this group and they are known to generations of school students for the “Pythagorean theorem”. Before getting started on the various proofs, let us make it clear that other cultures (Egypt, Mesopotamia, India) way before the Greeks knew of versions of the Pythagorean theorem (a^2 + b^2 = c^2). Did Pythagoras discover this theorem himself? Perhaps his followers discovered it and attributed it to him. Maybe Pythagoras only provided a proof of something observed for quite some time. Did the other cultures know a proof? The debate continues.
Theorem (The Pythagoreans): If a right triangle has legs which measure A and B and hypotenuse which measures C, then A^2 + B^2 = C^2.
Amazingly there are several hundred proofs of this theorem. Let us demonstrate a few of them.
Proof 1 (using a dissection method possibly used by the Pythagoreans)
Start with the following right triangle:
Make four exact copies of this triangle and arrange them as in the picture below:
The area of the above square is C^2. Now arrange the above pieces (which does not change the area!) into the picture below
Convince yourself that on either sides of the red line you have two squares (Why?). The square on the left of the red line has area A^2 and the square in the right has area B^2. So the total area is A^2 + B^2. However, we just computed the area above as C^2. Thus A^2 + B^2 = C^2. QED.
Proof 2 (another dissection method)
Start with a right triangle.
Now consider the following square.
Take the four triangles in the above picture and arrange them in a new drawing as follows:
In the above drawing, the area excluding the four triangles is C^2. In the one just before it, the area excluding the four triangles is A^2 + B^2. Since these two areas are the same, it must be the case that A^2 + B^2 = C^2. QED.
Proof 3 (Proof in Euclid’s elements – also known as the “Bride’s chair proof”)
This proof is the most complicated of the proofs we will do. To start we need a two elementary facts:
Fact 1: If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent
Fact 2: The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
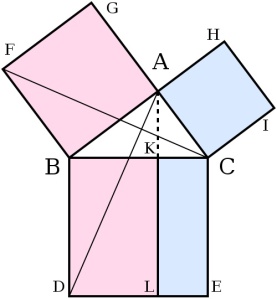
Consider the right triangle ABC with a right angle at vertex A. The following diagram is known as “The famous figure of Pythagoras”.
Let ACB be a right-angled triangle with right angle CAB.
On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order.
From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
Join CF and AD, to form the triangles BCF and BDA.
Angles CAB and BAG are both right angles; therefore C, A, and G are colinear. Similarly for B, A, and H.
Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
Since AB and BD are equal to FB and BC, respectively, triangle ABD must be congruent to triangle FBC (Fact 1)
Since A is colinear with K and L, rectangle BDLK must be twice in area to triangle ABD (Fact 2)
Since C is colinear with A and G, square BAGF must be twice in area to triangle FBC (Fact 2)
Therefore rectangle BDLK must have the same area as square BAGF = AB2.
Similarly, it can be shown that rectangle CKLE must have the same area as square ACIH = AC2.
Adding these two results, AB2 + AC2 = BD × BK + KL × KC
Since BD = KL, BD* BK + KL × KC = BD(BK + KC) = BD × BC
Therefore AB2 + AC2 = BC2, since CBDE is a square. QED.
Proof 4: (by President James Garfield)
Garfield’s proof starts with the following drawing:
The area of a trapezoid is Area = 1/2 (base) (height_1 + height_2)
In the above diagram, base=a+b, height_1 =a, and height_2 =b.
Thus the area is A = (1/2)(a^2+2ab+b^2).
Let’s find the area of the trapezoid by summing the area of the three right triangles.
The area of the yellow triangle is A_yellow =1/2(ba).
The area of the red triangle is A_red =1/2(c^2).
The area of the blue triangle is A_blue= 1/2(ab).
The sum of the area of the triangles is
1/2(ba) + 1/2(c^2) + 1/2(ab) = 1/2(ba + c^2 + ab) = 1/2(2ab + c^2).
Since, this area is equal to the area of the trapezoid we have the following relation:
(1/2)(a^2 + 2ab + b^2) = (1/2)(2ab + c^2).
Multiplying both sides by 2 and subtracting 2ab from both sides we get a^2 + b^2 = c^2 QED.
Pythagorean triples: These are triples of whole numbers a, b, c so that a^2 + b^2 = c^2. For example, a = 2, b = 3, c = 5 is a Pythagorean triple. Another is a = 36, b = 77, c = 85.
Are there an infinite number of Pythagorean triples?
Theorem (Euclid): There are an infinite number of Pythagorean triples.
Proof: For each integer m greater than 1, notice that a = m^2 – 1, b = 2 m, c = m^2 + 1 satisfies a^2 + b^2 = c^2. This yields an infinite number of Pythagorean triples — one for each m. QED.
Note: Euclid goes further an characterizes all of the Pythagorean triples. I’ll let you investigate this on your own.
√2 is irrational! There was some trouble amongst the Pythagorean faithful, who earnestly believed that one could understand the universe through ratios of integers, when it was discovered that √2 could not. Real numbers which can be written as the quotient of integers are called rational – e.g., (1/2, 2/3, 98, 115, etc.). Real numbers which are not the ratio of integers are called irrational.
Theorem (The Pythagoreans): √2 is irrational
Proof: Here is a new proof technique for us. It is called “proof by contradiction” or reductio ad absurdum (reduce to absurdity). First note that if m is odd then m^2 is also odd. Indeed if m = 2 k + 1, then m^2 = (2 k + 1)^2 = 4 k^2 + 4 k + 1 which is odd. Using the fact that P implies Q means that not Q implies not P (this is called contraposition) we see that n^2 is even implies that n is even.
Now onto the proof. Suppose that √2 were indeed rational.Then √2 = m/n for two integers m and n which we assume have no common factor. If they have a common factor – divide it out. Then, squaring both sides of the equality √2 = m/n, we get 2 = m^2/n^2 and so m^2 = 2 n^2. This last statement says that m^2 is even. By the remark at the beginning of the proof, we see that m is even. But if m if even then m = 2 k and thus, going back to the identity m^2 = 2 n^2, we get (2 k)^2 = 2 n^2 or, after working the algebra, 2 k^2 = n^2. Thus n^2 is even. Again appealing to the discussion at the beginning of the proof, we get that n is even. This means that both m and n are even, which means they have a common factor of 2. Now we have a contradiction to the fact that m and n have no common factors. QED.
Note: To the uninitiated, this seems like a strange way to prove something — assume what you are trying to prove is false and then following the logic until you get something ridiculous. However, in natural arguments, you do this all the time! Think about it. A friend, in an argument you are having, says something you know is not true. You tell your friend “OK. If you believe what you just said is true then you must believe this is true. But then you must believe this is true, etc…”. At the end you deduce that what your friend said at the beginning of your argument implies, through the steps of deduction, something everybody — including your friend – knows is false. Reductio ad absurdum is a very effective proof technique in mathematics and was used by the Greeks on numerous occasions and is still used today.
Note: Irrational numbers exist in abundance. For example, Theodorus of Cyrene showed that √3, √5, √6, √7, √8, √10, √11, √12, √13, √14, √15, √17 are all irrational. In fact there is a famous spiral names after him and gives a way of constructing the square roots of all of the integers (with a ruler with a length of 1 and a compass).
Theodorous stopped at 17 (nobody know why). E. Teuffe proved in 1958 that no two hypotenuses will ever coincide, regardless of how far the spiral is continued.
The number π is also irrational. We will discuss this later on.
Pythagorean legends:
- The Pythagoreans were quite disturbed to find out that √2 was irrational and tried to keep is a secret since it went opposite their world view that everything could be understood as ratios of integers. One legend claims that one of the Pythagoreans named Hippasus was executed by the brotherhood for telling others outside the brotherhood of this scandal. Another legend claims he was banished from the group and an empty tomb was erected to let him know that he was considered dead to them.
- Pythagoras is rumored to have sacrificed an ox (perhaps several) after his discovery of the Pythagorean theorem.
- The Greek writer Iamblichus of Chalcis wrote a biography of Pythagoras called Pythagorean Life which has many elaborate and fantastic (i.e., probably not true!) stories of Pythagoras and his followers.
- The Pythagoreans believed in reincarnation and that one was doomed to an endless existence of moving from one living creature to another unless one could gain the understanding of nature and the divine. This much is true. What is probably not true is the claim that Pythagoras could recall all of his past lives.
- There are also stories about Pythagoras and his refusal to eat beans — don’t ask!
- Pythagoras is rumored to have invented the Pythagorean cup which prevents someone from drinking too much.
We will end our discussion of Pythagoras with a famous statue of him built in the harbor of his Greek island home of Samos. Does this statue capture Pythagoras and the Pythagorean spirit?
Here is the same statue from a different view
Here is one more view.